DOMANDA di Valentina e Simone
In un trapezio rettangolo ABCD la diagonale minore AC è perpendicolare al lato obliquo BC. Sapendo che l’altezza CH supera di 3 cm la base minore CD e che la base maggiore AB è uguale al triplo della minore diminuito di 2 cm, calcola l’area del trapezio ABCD e il suo perimetro.
RISPOSTA:
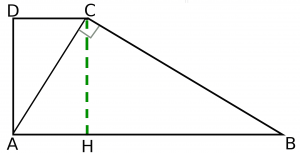
Scriviamo i dati che il problema ci fornisce facendo riferimento alla figura riportata di seguito:
- $A\hat{C}B = 90^\circ$
- $\overline{CH} = \overline{AD} = \overline{CD} + 3\text{ cm}$;
- $\overline{AB} = 3\cdot\overline{CD} – 2\text{ cm}$;
Utilizzando i dati che il problema ci fornisce dobbiamo calcolare l’area e il perimetro del trapezio $ABCD$.
Poniamo $\overline{CD}=x$. Per costruzione si ha che:
$\overline{AH}=\overline{CD} = x$;
Di conseguenza si ha che:
$\overline{BH} = \overline{AB} – \overline{AH} =3\cdot x – 2\text{ cm} – x = 2x – 2\text{ cm}$.
Per poter calcolare la nostra incognita $x$ bisogna impostare un’equazione e risolverla. Tale equazione può essere impostata applicando il secondo teorema di Euclide (in un triangolo rettangolo l’altezza relativa all’ipotenusa è medio proporzionale tra le proiezioni dei cateti sull’ipotenusa) al triangolo rettangolo ABC. Possiamo quindi scrivere la seguente proporzione:
$\overline{AH}:\overline{CH}=\overline{CH}:\overline{BH}$;
$ x : (x+3)=(x+3):(2x-2)$;
In una proporzione il prodotto degli interni è uguale a quello degli esterni, quindi:
$(x+3)^2= x\cdot (2x-2)$;
$x^2+9+6x=2x^2-2x$;
$2x^2 – 2x – x^2 – 6x – 9=0$;
$x^2-8x-9=0$;
Abbiamo così ottenuto un’equazione di secondo grado le cui soluzioni sono:
$x_1 = \dfrac{8-\sqrt{64 + 4\cdot 9}}{2} = \dfrac{8-\sqrt{100}}{2} = \dfrac{8-10}{2} = \dfrac{-2}{2} = -1$;
$x_2 = \dfrac{8+\sqrt{64 + 4\cdot\ 9}}{2} = \dfrac{8+\sqrt{100}}{2} = \dfrac{8+10}{2} = \dfrac{18}{2} = 9$.
Poichè $x=\overline{CD}$ è la misura di un lato del trapezio, non può essere negativa, quindi la soluzione $x_1 = -1$ non è accettabile. Pertanto possiamo scrivere che:
$\overline{CD} = x = 9\text{ cm}$;
Di conseguenza si ha che:
$\overline{CH} = \overline{AD} = \overline{CD} + 3\text{ cm} = \left(9+3\right)\text{ cm} = 12\text{ cm}$;
$\overline{AB} = 3\cdot\overline{CD} – 2\text{ cm} = \left(3\cdot 9 – 2\right)\text{ cm}= 25\text{ cm}$;
$\overline{BH} = \overline{AB} – \overline{AH} = (25 – 9)\text{ cm} = 16\text{ cm}$.
Per calcolare il lato obliquo $\overline{BC}$ applichiamo il teorema di Pitagora (in un triangolo rettangolo l’ipotenusa elevata al quadrato è uguale alla somma dei cateti elevati al quadrato) al triangolo rettangolo $BCH$:
$\overline{BC} = \sqrt{\overline{BH}^{2} \; \text{+} \; \overline{CH}^{2}}$;
$\overline{BC} =\sqrt{\left(16^2 + 12^2 \right)\text{ cm}^2} = \sqrt{\left(256 + 144\right)\text{ cm}^2} = \sqrt{400\text{ cm}^2} = 20\text{cm}$;
A questo punto possiamo calcolare perimetro e area del trapezio:
$P_{ABCD}=\overline{AB}+\overline{BC}+\overline{CD}+\overline{AD}= \left(25 + 20 + 9 + 12\right)\text{ cm} = 66\text{ cm}$;
$A_{ABCD}=\dfrac{\left(\overline{AB}+\overline{CD}\right)\cdot\;\overline{CH}}{2}=\dfrac{\left(25+9\right)\cdot\;12}{2}\text{ cm}^2=204\text{ cm}^2$